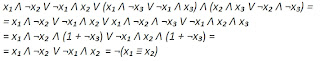ЕГЭ-2013. Задание В15. Логические уравнения

11 мая 2013
Условие 3: Сколько существует различных наборов значений логических переменных x₁, x₂, x₃, ..., x₇, x₈ x₉, которые удовлетворяют всем перечисленным ниже условиям? 

В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

Решение:

1)  Выполним преобразование логического выражения первого уравнения

Аналогично для второго, третьего и четвертого уравнений.

2) Система уравнений принимает следующий вид:

3) Каждое уравнение имеет два решения. Четыре уравнения независимы друг от друга, поэтому система из четырех уравнений имеет 2·2·2·2 =16 решений.

4) В процессе преобразования (п.1) логических выражений исходной системы уравнений сократилась логическая переменная  x₉. Следовательно, количество наборов значений логических переменных x₁, x₂, x₃, ..., x₇, x₈  удваивается,  т.е. 16 · 2 = 32.

Ответ: 32.


7  мая 2013
Условие 2: Сколько существует различных наборов значений логических переменных x₁, x₂, x₃, ..., x₇, x₈, которые удовлетворяют всем перечисленным ниже условиям? 

В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

Решение (метод замены переменных):
1)  Выполним преобразование первого уравнения

 И далее всех остальных.

2) Сделаем замену

 

3) Система примет следующий вид

4) Найдем решения полученной системы логических уравнений. Два набора логических переменных y₁, y₂, y₃, y₄ (0,0,0,0) и (1,1,1,1) являются решениями данной системы.

5)   Найдем наборы исходных переменных х₁ и х₂, при которых  ¬ x₁ V x₂ = 0  и ¬ x₁ V x₂ = 1.  

¬ x₁ V x₂ = 0  при одном наборе (1,0).

¬ x₁ V x₂ = 1 при трёх наборах (0,0), (0,1) и (1,1).

Аналогично для остальных наборов переменных х₃ и х₄, х₅ и х₆, х₇ и х₈. 

6) Для набора логических переменных y₁, y₂, y₃, y₄ (0,0,0,0) имеем 1 вариант набора переменных x₁, x₂, x₃, …, x₇, x₈.  Для набора логических переменных y₁, y₂, y₃, y₄ (1,1,1,1) имеем 3*3*3*3 = 81  вариант набора переменных x₁, x₂, x₃, …, x₇, x₈.  

7) Складываем результаты: 1 + 81 = 82.

Ответ: 82.

18 марта 2013
Условие 1: Сколько существует различных наборов значений  логических переменных x₁, x₂, x₃, x₄, x₅, y₁, y₂, y₃, y₄, y₅ , которые удовлетворяют всем перечисленным ниже условиям? 

 В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

Решение:

1) Первые два уравнения независимы друг от друга (в первое входят только x₁, x₂, …, x₅, а во второе – только y₁, y₂, …, y₅)

2) Третье уравнение связывает первые два, поэтому можно поступить так:

·    найти решения первого уравнения

·    найти решения второго уравнения

·    найти множество решений первых двух уравнений

·    из множества решений первых двух уравнений убрать решения, которые не удовлетворяют третьему уравнению

3) Найдем решения первого уравнения: 

(x₁, x₂, x₃, x₄, x₅) = 00000     00001     00011    00111     01111     11111

4) Второе решение имеет аналогичный набор:

(y₁, y₂, y₃, y₄, y₅) = 00000     00001     00011    00111     01111     11111

5) Первые два уравнения независимы друг от друга, поэтому система из первых двух уравнений имеет 6·6=36 решений: каждому решению первого соответствует 6 разных комбинаций переменных y₁, y₂, …, y₅, которые решают второе, и наоборот, каждому решению второго соответствует 6 разных комбинаций переменных x₁, x₂, …, x₅, которые решают первое:

(x1, x2, x3, x4, x5)	=	00000	00001	00011	00111	01111	11111
(y1, y2, y3, y4, y5)	=	00000	00000	00000	00000	00000	00000
		00001	00001	00001	00001	00001	00001
		00011	00011	00011	00011	00011	00011
		00111	00111	00111	00111	00111	00111
		01111	01111	01111	01111	01111	01111
		11111	11111	11111	11111	11111	11111

6) Третье уравнение можно представить в виде:

7) Импликация в первой скобке ложна только для y₁ = 1 и x₁ = 0, следовательно, такая комбинация нарушает третье уравнение. Набору с y₁ = 1 (y₁, y₂, y₃, y₄, y₅) = 11111  соответствует, с учетом третьего уравнения, только одно решение первого, в котором x₁ = 1 (x₁, x₂, x₃, x₄, x₅) = 11111. Множество решений имеет следующий вид:

(x1, x2, x3, x4, x5)	=	00000	00001	00011	00111	01111	11111
(y1, y2, y3, y4, y5)	=	00000	00000	00000	00000	00000	00000
		00001	00001	00001	00001	00001	00001
		00011	00011	00011	00011	00011	00011
		00111	00111	00111	00111	00111	00111
		01111	01111	01111	01111	01111	01111
							11111

 8) Рассуждая таким образом для остальных частей третьего уравнения,  множество приобретает следующий вид:

(x1, x2, x3, x4, x5)	=	00000	00001	00011	00111	01111	11111
(y1, y2, y3, y4, y5)	=	00000	00000	00000	00000	00000	00000
			00001	00001	00001	00001	00001
				00011	00011	00011	00011
					00111	00111	00111
						01111	01111
							11111

9) Итого имеем 21 решение.

Ответ: 21.